In C, searching is an algorithm which helps us to search elements in a given set of elements. The element may be a record, a table, or a file.
Any search is said to be successful or unsuccessful depending upon whether the element that is being searched is found or not. Some of the standard searching technique that is being followed in data structure is listed below:
In this type of search, a sequential search is made over all items one by one. Every item is checked and if a match is found then that particular item is returned, otherwise the search continues till the end of the data collection.
This method can be performed on a sorted or an unsorted list (usually arrays). In case of a sorted list searching starts from 0th element and continues until the element is found from the list or the element whose value is greater than (assuming the list is sorted in ascending order), the value being searched is reached.
As against this, searching in case of unsorted list also begins from the 0th element and continues until the element or the end of the list is reached.
Linear Search Flow Chart:
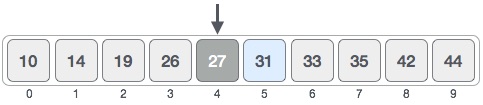 Now we compare the value stored at location 4, with the value being searched, i.e. 31. We find that the value at location 4 is 27, which is not a match. As the value is greater than 27 and we have a sorted array, so we also know that the target value must be in the upper portion of the array.
Now we compare the value stored at location 4, with the value being searched, i.e. 31. We find that the value at location 4 is 27, which is not a match. As the value is greater than 27 and we have a sorted array, so we also know that the target value must be in the upper portion of the array.
 We change our low to mid + 1 and find the new mid value again.
We change our low to mid + 1 and find the new mid value again.
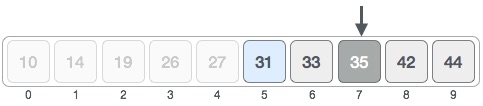 The value stored at location 7 is not a match, rather it is more than what we are looking for. So, the value must be in the lower part from this location.
The value stored at location 7 is not a match, rather it is more than what we are looking for. So, the value must be in the lower part from this location.
 Hence, we calculate the mid again. This time it is 5.
Hence, we calculate the mid again. This time it is 5.
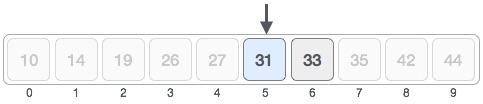 We compare the value stored at location 5 with our target value. We find that it is a match.
We compare the value stored at location 5 with our target value. We find that it is a match.

We conclude that the target value 31 is stored at location 5.
Binary search halves the searchable items and thus reduces the count of comparisons to be made to very less numbers.
Binary Search Flowchart:
Binary Search Pseudocode:
Procedure binary_search
A ← sorted array
n ← size of array
x ← value to be searched
Set lowerBound = 1
Set upperBound = n
while x not found
if upperBound < lowerBound
EXIT: x does not exists.
set midPoint = lowerBound + ( upperBound - lowerBound ) / 2
if A[midPoint] < x
set lowerBound = midPoint + 1
if A[midPoint] > x
set upperBound = midPoint - 1
if A[midPoint] = x
EXIT: x found at location midPoint
end while
end procedure
Binary Search Code:
⇒Binary Search C:http://bit.ly/2KnBU2u
⇒Binary Search Java:http://bit.ly/2G63tt9
⇒Binary Search python:http://bit.ly/2Uw2jPP
Binary Search Complexity:
Any search is said to be successful or unsuccessful depending upon whether the element that is being searched is found or not. Some of the standard searching technique that is being followed in data structure is listed below:
- Linear Search or Sequential Search
- Binary Search
What is Linear Search?
This method can be performed on a sorted or an unsorted list (usually arrays). In case of a sorted list searching starts from 0th element and continues until the element is found from the list or the element whose value is greater than (assuming the list is sorted in ascending order), the value being searched is reached.
As against this, searching in case of unsorted list also begins from the 0th element and continues until the element or the end of the list is reached.
Linear Search Flow Chart:
Linear Search algorithm:
Linear Search ( Array A, Value x)
Step 1: Set i to 1
Step 2: if i > n then go to step 7
Step 3: if A[i] = x then go to step 6
Step 4: Set i to i + 1
Step 5: Go to Step 2
Step 6: Print Element x Found at index i and go to step 8
Step 7: Print element not found
Step 8: Exit
⇒Linear Search C:http: http://bit.ly/2IhyR9q
⇒Linear Search Java: http://bit.ly/2FU8OCI
⇒Linear Search Python:http://bit.ly/2I3dyJK
Linear Search Complexity:
Worst-case space complexity: O(1)
iterative Worst-case performance: O(n)
Best-case performance: O(1)
Average performance: O(n)
What is Binary Search?
Binary search is a fast search algorithm with run-time complexity of Ο(log n). This search algorithm
works on the principle of divide and conquer.It requires the list to be in sorted order. In this
method, to search an element you can compare it with the present element at the center of the list. If it matches, then the search is successful otherwise the list is divided into two halves: one from the 0th element to the middle element which is the center element (first half) another from the center element to the last element (which is the 2nd half) where all values are greater than the center element.
Binary Search Example Step by Step:
The following is our sorted array and let us assume that we need to search the location of value 31 using binary search.
 First, we shall determine half of the array by using this formula −
First, we shall determine half of the array by using this formula −
The following is our sorted array and let us assume that we need to search the location of value 31 using binary search.

mid = low + (high - low) / 2
Here it is, 0 + (9 - 0 ) / 2 = 4 (integer value of 4.5). So, 4 is the mid of the array.

low = mid + 1
mid = low + (high - low) / 2
Our new mid is 7 now. We compare the value stored at location 7 with our target value 31.



We conclude that the target value 31 is stored at location 5.
Binary search halves the searchable items and thus reduces the count of comparisons to be made to very less numbers.
Binary Search Flowchart:
Binary Search Pseudocode:
Procedure binary_search
A ← sorted array
n ← size of array
x ← value to be searched
Set lowerBound = 1
Set upperBound = n
while x not found
if upperBound < lowerBound
EXIT: x does not exists.
set midPoint = lowerBound + ( upperBound - lowerBound ) / 2
if A[midPoint] < x
set lowerBound = midPoint + 1
if A[midPoint] > x
set upperBound = midPoint - 1
if A[midPoint] = x
EXIT: x found at location midPoint
end while
end procedure
Binary Search Code:
⇒Binary Search C:http://bit.ly/2KnBU2u
⇒Binary Search Java:http://bit.ly/2G63tt9
⇒Binary Search python:http://bit.ly/2Uw2jPP
Binary Search Complexity:
- Best-case performance O(1)
- Average performance O(log n)
- Worst-case space complexity O(1)


No comments:
Post a Comment