Binary Search Tree is a binary tree in which every node contains only smaller values in its left subtree and only larger values in its right subtree.
- It is called a binary tree because each tree node has maximum of two children.
- It is called a search tree because it can be used to search for the presence of a number in
O(log(n))time.
The properties that separates a binary search tree from a regular binary tree is
- All nodes of left subtree are less than root node
- All nodes of right subtree are more than root node
- Both subtrees of each node are also BSTs i.e. they have the above two properties
Operations on a Binary Search Tree
The following operations are performed on a binary search tree...
- Search
- Insertion
- Deletion
Search Operation in BST
In a binary search tree, the search operation is performed with O(log n) time complexity. The search operation is performed as follows...
- Read the search element from the user.
- Compare the search element with the value of root node in the tree.
- If both are matched, then display "Given node is found!!!" and terminate the function
- If both are not matched, then check whether search element is smaller or larger than that node value.
- If search element is smaller, then continue the search process in left subtree.
- If search element is larger, then continue the search process in right subtree.
- Repeat the same until we find the exact element or until the search element is compared with the leaf node
- If we reach to the node having the value equal to the search value then display "Element is found" and terminate the function.
- If we reach to the leaf node and if it is also not matched with the search element, then display "Element is not found" and terminate the function.
Insertion Operation in BST
In a binary search tree, the insertion operation is performed with O(log n) time complexity. In binary search tree, new node is always inserted as a leaf node. The insertion operation is performed as follows...
- Create a newNode with given value and set its left and right to NULL.
- Check whether tree is Empty.
- If the tree is Empty, then set root to newNode.
- If the tree is Not Empty, then check whether the value of newNode is smaller or larger than the node (here it is root node).
- If newNode is smaller than or equal to the node then move to its left child. If newNode is larger than the node then move to its right child.
- Repeat the above steps until we reach to the leaf node (i.e., reaches to NULL).
- After reaching the leaf node, insert the newNode as left child if the newNode is smaller or equal to that leaf node or else insert it as right child.
Deletion Operation in BST
In a binary search tree, the deletion operation is performed with O(log n) time complexity. Deleting a node from Binary search tree includes following three cases...
- Deleting a Leaf node (A node with no children)
- Deleting a node with one child
- Deleting a node with two childreneft subtree
There are two basic operations that you can perform on a binary search tree:
1. Check if number is present in binary search tree
The algorithm depends on the property of BST that if each left subtree has values below root and each right subtree has values above root.
If the value is below root, we can say for sure that the value is not in the right subtree; we need to only search in the left subtree and if the value is above root, we can say for sure that the value is not in the left subtree; we need to only search in the right subtree.
Algorithm:
If root == NULL
return NULL;
If number == root->data
return root->data;
If number < root->data
return search(root->left)
If number > root->data
return search(root->right)
Let us try to visualize this with a diagram.
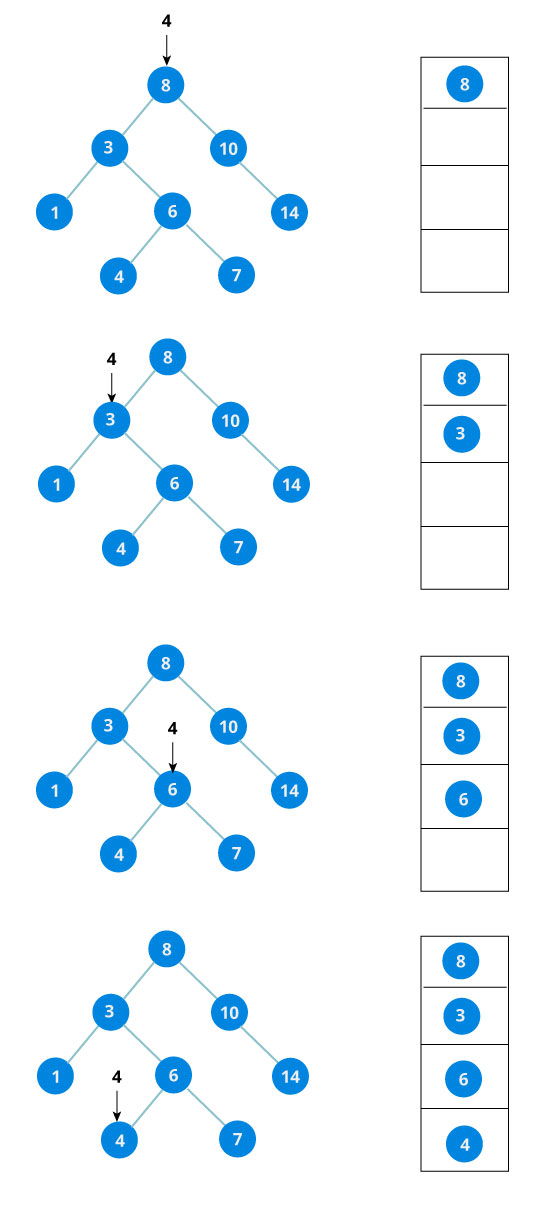 If the value is found, we return the value so that it gets propogated in each recursion step as shown in the image below.
If you might have noticed, we have called return search(struct node*) four times. When we return either the new node or NULL, the value gets returned again and again until search(root) returns the final result.
If the value is found, we return the value so that it gets propogated in each recursion step as shown in the image below.
If you might have noticed, we have called return search(struct node*) four times. When we return either the new node or NULL, the value gets returned again and again until search(root) returns the final result.
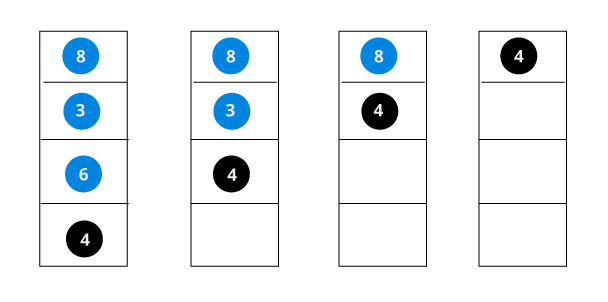 If the value is not found, we eventually reach the left or right child of a leaf node which is NULL and it gets propagated and returned.
If the value is not found, we eventually reach the left or right child of a leaf node which is NULL and it gets propagated and returned.
If root == NULL
return NULL;
If number == root->data
return root->data;
If number < root->data
return search(root->left)
If number > root->data
return search(root->right)

2. Insert value in Binary Search Tree(BST)
Inserting a value in the correct position is similar to searching because we try to maintain the rule that left subtree is lesser than root and right subtree is larger than root.
We keep going to either right subtree or left subtree depending on the value and when we reach a point left or right subtree is null, we put the new node there.
Algorithm:
If node == NULL
return createNode(data)
if (data < node->data)
node->left = insert(node->left, data);
else if (data > node->data)
node->right = insert(node->right, data);
return node;
The algorithm isn't as simple as it looks. Let's try to visualize how we add a number to an existing BST.
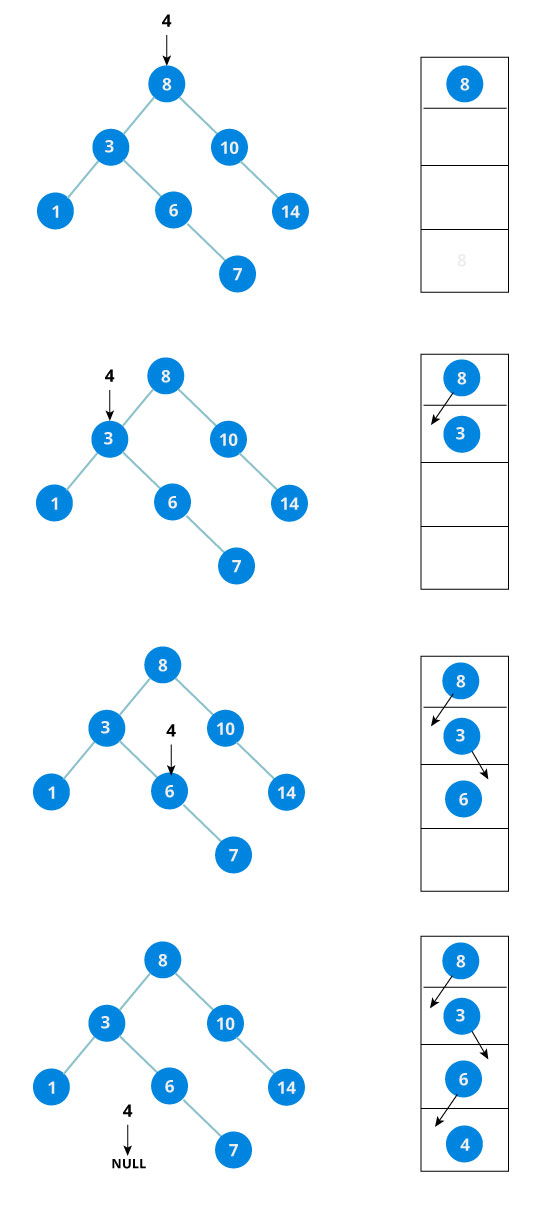 We have attached the node but we still have to exit from the function without doing any damage to the rest of the tree. This is where the
We have attached the node but we still have to exit from the function without doing any damage to the rest of the tree. This is where the return node; at the end comes in handy. In the case of NULL, the newly created node is returned and attached to the parent node, otherwise the same node is returned without any change as we go up until we return to the root.
This makes sure that as we move back up the tree, the other node connections aren't changed.
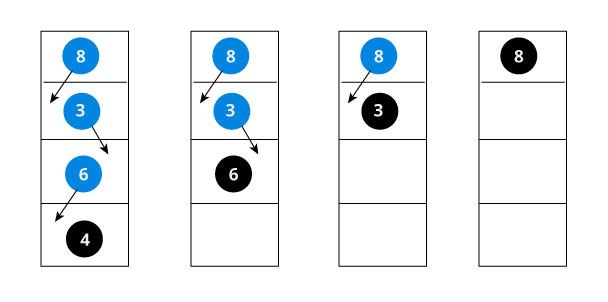
If node == NULL
return createNode(data)
if (data < node->data)
node->left = insert(node->left, data);
else if (data > node->data)
node->right = insert(node->right, data);
return node;
return node; at the end comes in handy. In the case of NULL, the newly created node is returned and attached to the parent node, otherwise the same node is returned without any change as we go up until we return to the root.
No comments:
Post a Comment